
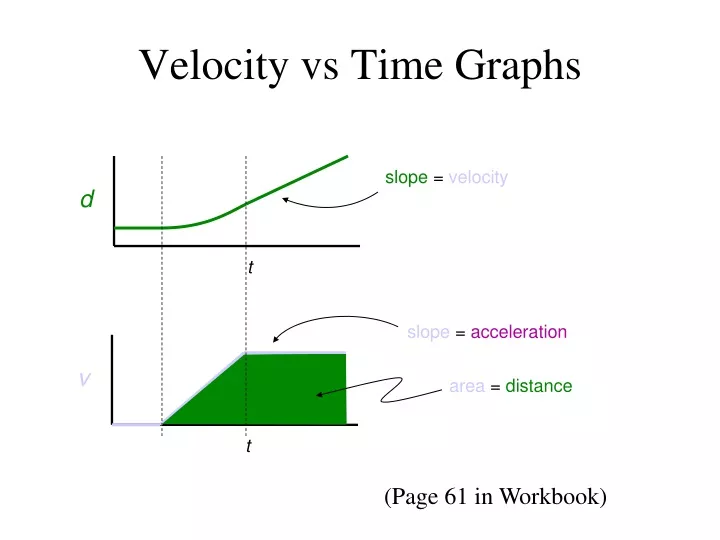
Therefore the total distance travelled was 900m. You can then simply add the areas together and the total area represents the total distance travelled.Į.g. Calculate the area of each shape as shown below. Start by dividing the graph into sections that consist of simple triangles and rectangles as shown below in blue and red. The total distance travelled by an object can be determined by calculating the area underneath the velocity time graph. =Calculating the Distance Travelled from a Velocity-Time Graph= The average acceleration can be calculated for any part of a journey by taking the '''change in velocity''' and dividing by the '''change in time''' for that part of the journey.
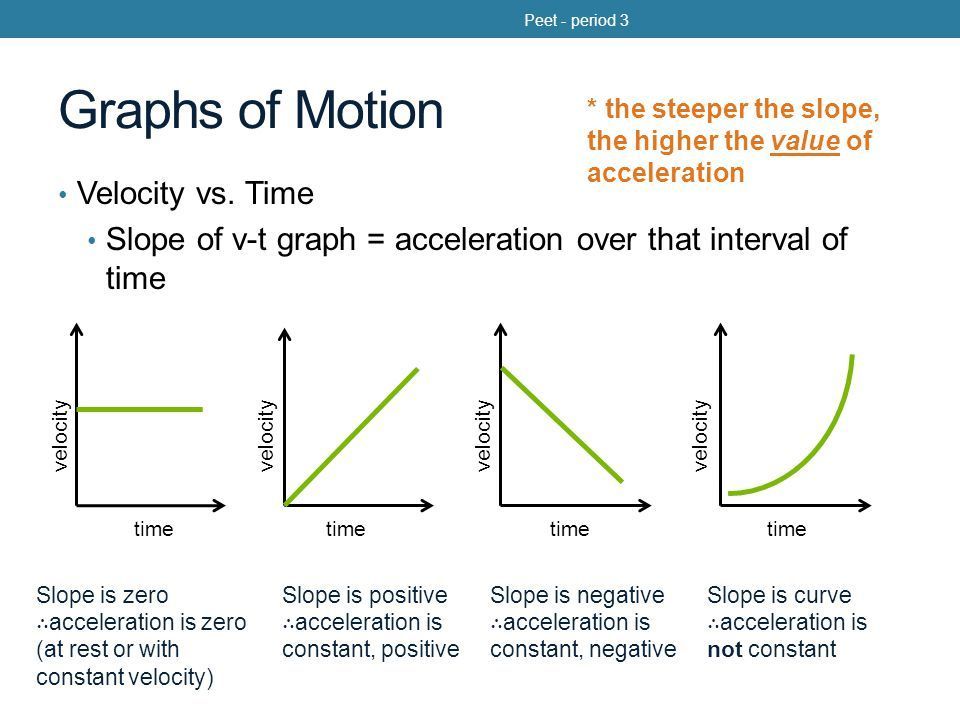
=Calculating Acceleration from a Velocity-Time Graph= The general rule of thumb is if the object is going from a high speed to a low speed, it is decelerating. The negative value of the gradient gives the negative value for the acceleration (or deceleration), BUT, a negative value does not always mean slowing down! See the next section on ''''DIRECTION VECTORS'''' for elaboration.īe careful here. In the graph on the left, the line sloping upwards shows the object is '''accelerating''' and the line sloping downwards in this case towards v = 0, shows it is '''decelerating'''. On a velocity-time graph a '''horizontal (flat) line''' indicates the object is travelling at a '''constant speed'''.Ī '''straight diagonal line''' indicates the object's velocity is changing.


 0 kommentar(er)
0 kommentar(er)
